ABC is an equilateral triangle. Point P is on base BC such that PC = 1/3 BC, if AB = 6 cm find AP.

Given ABC is an equilateral triangle.
PC = (1/3) BC
PC = (1/3)×6 [BC = 6, side of equilateral triangle]
PC = 2
Construction:
Draw segment AD⊥BC

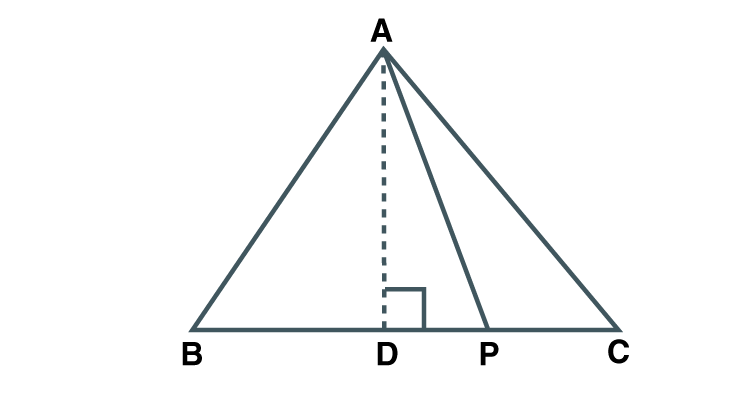
In ADC, C = 60˚
D = 90˚
CAD = 30˚
ADC is a 30˚- 60˚- 90˚triangle
AD = (√3/2)×AC [Side opposite to 60˚]
AD = (√3/2)×6
AD =3√3cm
DC = (1/2)BC [AD⊥BC]
DC = (1/2)×6 = 3cm
DC = DP+PC [D-P-C]
3 = DP +2
DP = 1
In ADP , D = 90˚
Applying Pythagoras theorem
AP² = AD²+DP²
AP² = (3√3)²+1²
AP² = 28
AP = 2√7 cm
Hence AP = 2√7cm.