Complete the following activity to find the sum of natural numbers from 1 to 140 which are divisible by 4.

The natural number divisible by 4 between 1 to 140 is
4, 8, 12, …….136
Where first term a = 4
Second term t₁ = 8
Third term t₂ = 12
Thus, common difference d = t₂ – t₁ = 12 – 8 = 4
t_n = 136
Now, by using n^th term of an A.P. formula
t_n = a + (n – 1) d
where n = no. of terms
a = first term
d = common difference
t_n = n^th terms
we can find value of “n” by substituting all the value in formula we get,
⇒ 136 = 4 + (n – 1) × 4
⇒ 136 – 4 = 4(n – 1)
⇒ 132 = 4(n – 1)
⇒ n – 1 = 132/4 = 33
⇒ n = 33 + 1 = 34
Now, by using sum of n^th term of an A.P. we will find its sum

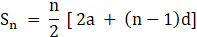
Where, n = no. of terms
a = first term
d = common difference
S_n = sum of n terms
Thus, substituting given value in formula we can find the value of S₃₄

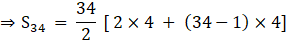
⇒S₃₄ = 17 × [8 + 33×4]
⇒S₃₄ = 17 × [8 + 132]
⇒S₃₄ = 17 × 140 = 2380
Thus, S₃₄ = 2380