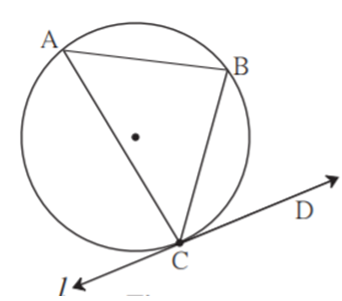
Analysis: As shown in the above figure, let line l be the tangent to the circle at point C. Line CB is a chord and CAB is an inscribed angle. Now by tangent- secant angle theorem, CAB BCD.
By converse of tangent- secant theorem, if we draw the line CD such that, CAB BCD, then it will be the required tangent.
Construction steps:
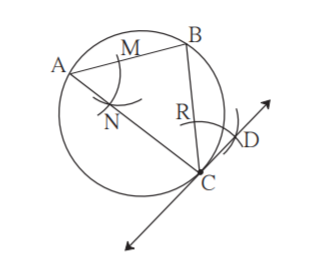
(1) Draw a circle of a radius 3.6 cm. Take any point C on it.
(2) Draw chord CB and an inscribed CAB .
(3) With the centre A and any convenient radius draw an arc intersecting the sides of BAC in points M and N.
(4) Using the same radius and centre C, draw an arc intersecting the chord CB at point R.
(5) Taking the radius equal to d(MN) and centre R, draw an arc intersecting the arc drawn in the previous step. Let D be the point of intersection of these arcs. Draw line CD. Line CD is the required tangent to the circle.