(1) The sum of the digits on the upper faces is at least 10.
Solution:
Given the sum of the digits on the upper faces is at least 10.
Probability of getting the sum of the digits on the upper faces is at least 10, p (A) =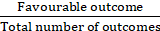
We know the favorable cases are (Where the Sum of digits on the upper faces is at least 10) = (4,6), (5,5), (5,6), (6,4), (6,5), (6,6) = 6 cases
Total Number of Outcomes = 36
p (A) = 6/36 = 1/6
(2) The sum of the digits on the upper faces is 33.
Solution:
Given the sum of the digits on the upper faces is 33.
Probability of getting the sum of the digits on the upper faces is 33, p (B) =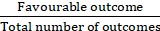
Favourable outcomes (Getting the sum of Digits on the upper Faces is 33) = 0 as the maximum sum could be 12
p(B) = 0
(3) The digit on the first die is greater than the digit on second die.
Solution:
Given the digit on the first die is greater than the digit on second die.
Probability of getting the digit on the first die is greater than the digit on second die, p(C) =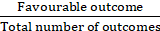
Favorable Outcomes are as follow = (2,1), (3,1), (3,2), (4,1), (4,2), (4,3), (5,1), (5,2), (5,3), (5,4), (6,1), (6,2), (6,3),(6,4), (6,5) = 15 cases
p(C) = 15/36 = 5/12
