In ABC, AB = 10, AC = 7, BC = 9 then find the length of the median drawn from point C to side AB

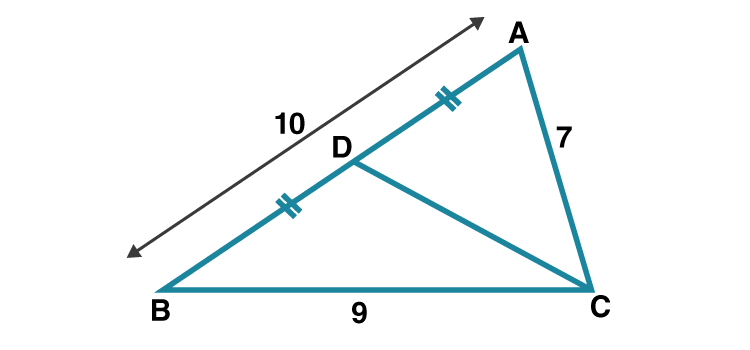
Let CD is the median drawn from C to AB.
Given AB = 10
AD = (1/2)×AB [D is the midpoint of side AB]
AD = 10/2 = 5
Since CD is the median
AC²+BC² = 2CD²+2AD² [Apollonius theorem]
7²+9² = 2 CD²+2×5²
2 CD² = 7²+9²-2×5²
2 CD² = 80
CD² = 40
Taking square roots on both sides
CD = 2√10
Hence the length of median drawn from point C to side AB is 2√10 units.