In figure 3.57, PQRS is cyclic. side PQ side RQ. PSR = 110°, Find

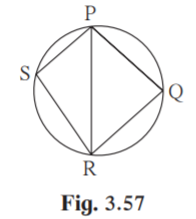
(1)Given PSR = 110˚
PQR = 180-110 = 70˚ [Opposite angles of a cyclic quadrilateral are supplementary.]
(2)PSR = ½ m(arc PQR) [The measure of an inscribed angle is half the measure of the arc intercepted by it]
m(arc PQR ) = 2×PSR
m(arc PQR ) = 2×110
m(arc PQR ) = 220˚
(3)Given side PQ side RQ
arc PQ arc RQ [Corresponding arcs of congruent chords of a circle are congruent. ]
m(arc PQ) = m(arc RQ)
M(arc PQR ) = m(arc PQ)+m(arc QR) [Property of sum of measures of arcs ]
220 = m(arc PQ)+m(arc QR)
m(arc PQ) = m(arc RQ) = 220/2 = 110˚
(4) m(arc PQ) = 110˚
PRQ = ½ m(arc PQ) [The measure of an inscribed angle is half the measure of the arc intercepted by it]
PRQ = ½ ×110
PRQ = 55˚