In figure 3.58, seg RS is a diameter of the circle with centre O. Point T lies in the exterior of the circle. Prove that RTS is an acute angle.

To prove : RTS is an acute angle.
Construction:
Join RT and ST. Let RT intersect circle at point A. Join AS.

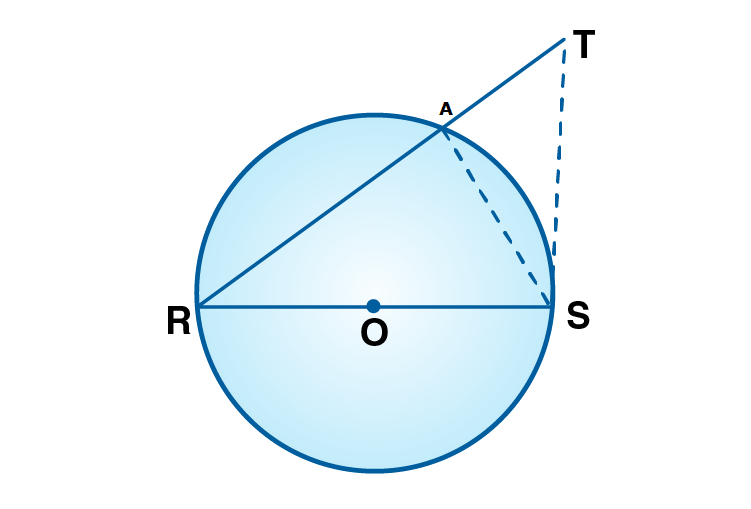
Proof:
Given RS is a diameter. O is the centre of the circle.
Since RS is the diameter , RAS = 90˚ [Angle in semi circle is right angle]
In ATS , RAS is an exterior angle and ATS is its remote interior angle.
RAS ATS [Exterior angle of a triangle is greater than remote interior angle]
90˚ATS
ATS 90˚
RTS 90˚ [ATS = RTS ]
RTS is acute.
Hence proved.