In figure 3.78, chord MN and chord RS intersect at point D.

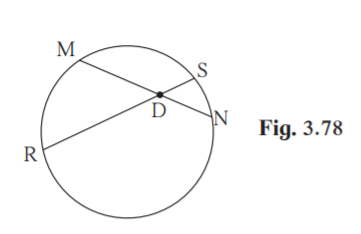
(1) Given RD = 15, DS = 4, MD = 8
RD×DS = MD×DN [Theorem of chords intersecting inside the circle]
15×4 = 8×DN
DN = 15×4/8 = 60/8
DN = 7.5 units
(2) RS = 18, MD = 9, DN = 8
RD×DS = MD×DN [Theorem of chords intersecting inside the circle]
(RS-DS)×DS = MD×DN [RD +DS = RS]
(18-DS)DS = 9×8
18DS -DS² = 72
DS²-18DS+72 = 0
Put DS = x
x²-18x+72 = 0
(x-6)(x-12) = 0
x = 6 or x = 12
DS = 6 or DS = 12 units