In figure 3.88, circles with centres X and Y touch internally at point Z . Seg BZ is a chord of bigger

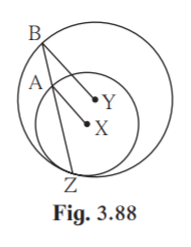
Given X and Y are the centres of the circle.
Proof:
Join YZ

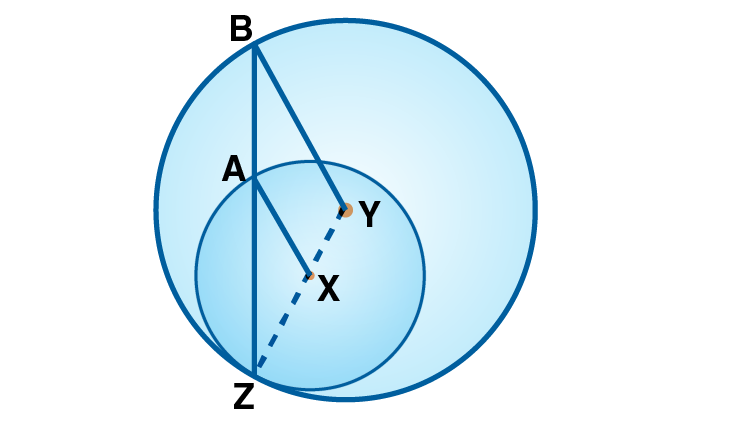
In AXZ ,
AX = XZ [Radii of same circle]
XAZ = XZA….(i) [Isoceles triangle theorem]
In BYZ,
YB = YZ [Radii of same circle]
YBZ = YZB [Isoceles triangle theorem]
XZA = YBZ ..(ii) [Y-X-Z, B-A-Z]
From (i) and (ii)
XAZ = YBZ
If a pair of corresponding angles formed by a transversal on two lines is congruent, then the two lines are
parallel.
seg AX seg BY [corresponding angles test]
Hence proved.