In figure 3.89, line l touches the circle with centre O at point P. Q is the mid point of radius OP. RS is a chord through Q such that chords RS || line l. If RS = 12 find the radius of the circle.

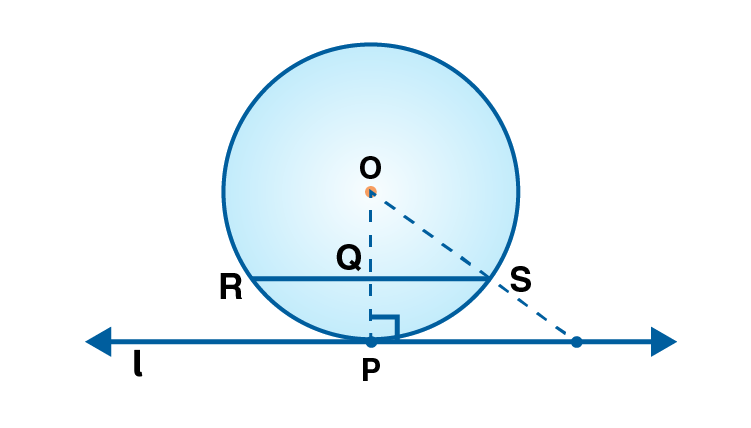
Given line l is a tangent.
Let the radius of circle be r.
OP is the radius.
OP line l. [Tangent theorem]
Given chord RSline l.
OP chord RS
Since the perpendicular from centre of the circle to the chord bisects the chord,
QS = ½ RS
QS = ½ ×12 = 6
OQ = r/2 [Given Q is the midpoint of OP]
In OQS
OS² = OQ²+QS² [Pythagoras theorem]
r² = (r/2)²+6²
r²-r²/4 = 36
(3/4)r² = 36
r² = 36×4/3
r²= 48
r = 4√3
Hence radius of circle is 4√3cm.