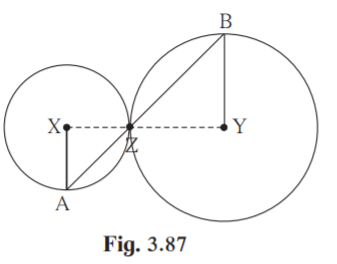
Construction: Draw segments XZ and YZ
Proof: By theorem of touching circles, points X, Z, Y are collinear.
XZA BZY vertically opposite angles
Let XZA = BZY = a ….. (I)
Now, seg XA seg XZ …….. (Radii of same circle)
XAZ = XZA. = a …….. (isosceles triangle theorem) (II)
similarly, seg YB seg YZ (Radii of same circle)
BZY = ZBY = a …….. (isosceles triangle theorem) (III)
from (I), (II), (III),
XAZ = ZBY
radius XA || radius YB ………. (Alternate angle test)
Question:
In the adjoining figure circles with centres X and Y touch each other at point Z. A secant passing
through Z intersects the circles at points A and B respectively. Prove that, radius XA || radius YB. Fill
in the blanks and complete the proof.
Construction: Draw segments XZ and ………. .
Proof: By theorem of touching circles, points X, Z, Y are ………. .
XZA ………. opposite angles
Let XZA = BZY = a ….. (I)
Now, seg XA seg XZ …….. (……….)
XAZ = ………. = a …….. (isosceles triangle theorem) (II)
similarly, seg YB ………. …….. (……….)
BZY = ………. = a …….. (……….) (III)
from (I), (II), (III),
XAZ = ……….
radius XA || radius YB ………. (……….)
Answer:
