In the adjoining figure, O is the centre of the circle. From point R, seg RM and seg RN are tangent segments touching the circle at M and N. If (OR) = 10 cm and radius of the circle = 5 cm, then

(1)Given RM and RN are the tangents to the circle.

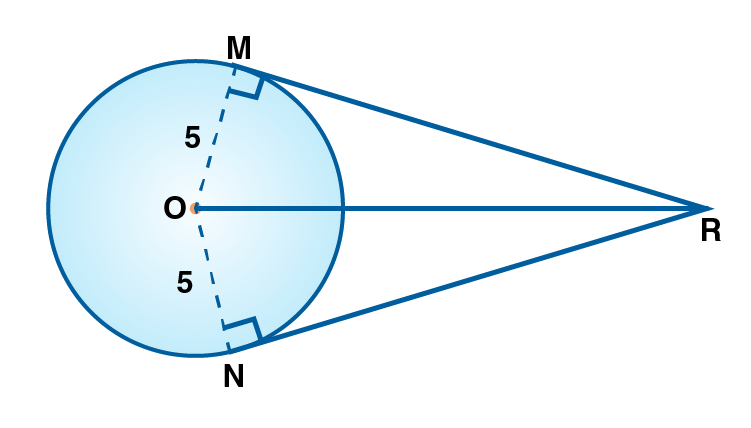
OMR = ONR = 90˚ [Tangent theorem]
In OMR , OR = 10 cm , [Given]
OM = 5cm [Radius]
OR² = OM²+MR² [Pythagoras theorem]
10² = 5²+MR²
MR² = 10²-5⁵
MR² = 75
MR = 5√3
RN = 5√3 [Tangent segments drawn from an external point to a circle are congruent]
(2)In OMR , OMR = 90˚ [Tangent theorem]
OM = 5cm [Radius]
OR = 10 cm [Given]
OM = ½ OR
MRO = 30˚ …(i) [Converse of 30˚- 60˚ -90˚ theorem]
NRO = 30˚……..(ii)
(3)MRN = MRO +NRO
MRN = 30+30 = 60˚ [from (i) and (ii)]