In the adjoining figure the radius of a circle with centre C is 6 cm, line AB is a tangent at A. Answer the following questions.

(1)Given AB is the tangent to the circle with centre C.
CAB = 90˚ [The tangent at any point of a circle is perpendicular to the radius through the point of contact.]
(2) Line AB seg CA. [Tangent theorem]
CA is the radius of the circle.
CA = 6cm
Distance of point C from AB is 6cm.
(3)In CAB , A = 90˚.

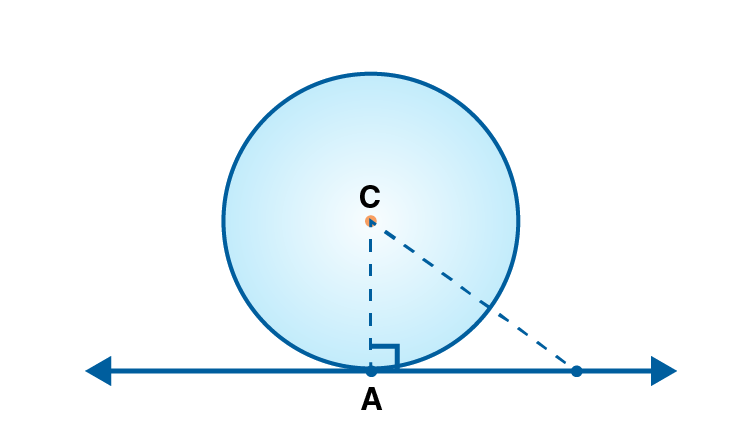
AC = 6 [radius]
AB = 6
BC² = AC²+AB² [Pythagoras theorem]
BC² = 6²+6²
BC² = 72
Taking square root on both sides
BC = √72 = 6√2 cm
d(B,C) = 6√2 cm.
(4)InABC , AB = AC = 6
ABC is an isosceles triangle.
Angles opposite two equal sides will be equal in isosceles triangle.
C = B……..(i)
A = 90˚ [Tangent theorem]
A + C +B = 180 [Angle sum property of triangle]
90+ C +B = 180
C +B = 90
C = B = 45˚ [From (i)]
ABC = 45˚