On 1st Jan 2016, Sanika decides to save ₹ 10, ₹ 11 on second day, ₹ 12 on third day. If she decides to save like this, then on 31st Dec 2016 what would be her total saving?

According to the question we can form an A.P.
10, 11, 12, 13, ……
Hence, the first term a = 10
Second term t₁ = 11
Third term t₂ = 12
Thus, common difference d = t₂ – t₁ = 12 – 11 = 1
Here, number of terms from 1^st Jan 2016 to 31^st Dec 2016 is,
n = 366
We need to find S₃₆₆
Now, by using sum of n^th term of an A.P. we will find its sum

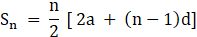
Where, n = no. of terms
a = first term
d = common difference
S_n = sum of n terms
Thus, on substituting the given value in formula we get,

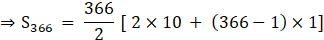
⇒S₃₆₆ = 183 [ 20 + 365]
⇒S₃₆₆ = 183 × 385
⇒S₃₆₆ = Rs 70,455