PQR ~ LTR. In PQR, PQ = 4.2 cm, QR = 5.4 cm, PR = 4.8 cm. Construct PQR and LTR, such that PQ/ LT = 3/4 .

Given PQR and LTR are similar.
Corresponding angles will be equal.
PRQ LRT
Given PQ/LT = 3/4
PQ/LT = QR/TR = PR/LR [Corresponding sides of similar triangles]
PQ/LT= QR/TR = PR/LR = 3/4
Sides of LTR are longer than corresponding sides of PQR.
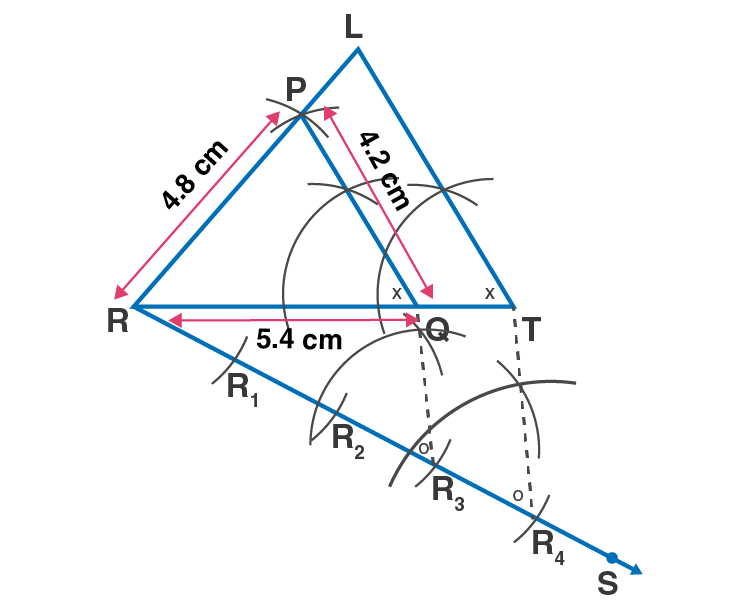
Steps of construction:
1. Draw ∆PQR such that PQ = 4.2 , QR = 5.4 , and PR = 4.8. Draw ray RS making an acute angle with side RQ.
2. Taking convenient distance on the compass, mark 4 points R₁, R₂, R₃, and R₄, such that RR₁ = R₁R₂ = R₂R₃ = R₃R₄.
3. Join QR₃. Draw a line parallel to QR₃ passing through R₄ to intersects ray RQ at T.
4. Draw a line parallel to side PQ through T. Name the point where parallel line intersect ray RP as L.
∆LTR is the required triangle similar to ∆PQR.