Select the appropriate alternative.

(1) In ABC and PQR, in a one to one correspondence AB/QR = BC/ PR = CA/ PQ then
(A) PQR ~ ABC
(B) PQR ~ CAB
(C) CBA ~ PQR
(D) BCA ~ PQR

Given AB/QR = BC/ PR = CA/ PQ
By SSS test of similarity , PQR ~ CAB .
Correct option is (B).

(2) If in DEF and PQR, D Q, R E then which of the following statements is
false?
(A) EF/PR = DF/ PQ
(B) DE/ PQ = EF/ RP
(C) DE/ QR = DF /PQ
(D) EF/ RP = DE/ QR

Solution:
Given D Q, R E
DEF ~QRP…. [AA test of similarity]
DE/QR = EF/RP = DF/QP [Corresponding sides of similar triangles]
DE/ PQ ≠ EF/ RP
Hence option (B) is false.

(3) In ABC and DEF B = E, F = C and AB = 3DE then which of the statements
regarding the two triangles is true?
(A)The triangles are not congruent and not similar
(B)The triangles are similar but not congruent.
(C)The triangles are congruent and similar.
(D) None of the statements above is true.

Solution:
Given B = E
F = C
ABC ~DEF [AA test of similarity]
Hence option B is the true statement.

(4) ABC and DEF are equilateral triangles, A (ABC):A(DEF)=1:2
If AB = 4 then what is length of DE?
(A)2√2
(B)4
(C)8
(D)4√2

Solution:
Given A (ABC):A(DEF) = 1:2
ABC and DEF are equilateral triangles.
A = D [Angle equals 60˚]
B = E [Angle equals 60˚]
ABC ~ DEF [AA test of similarity]
A (ABC):A(DEF) = AB²/DE² [Theorem of areas of similar triangles]
1/2 = 4²/DE²
Taking square root on both sides
1/√2 = 4/DE
DE = 4√2
Hence option (D) is the correct answer.

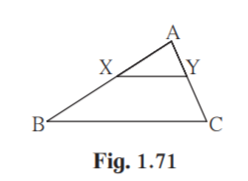
(5) In figure 1.71, seg XY || seg BC, then which of the following statements is true?
(A) AB / AC = AX / AY
(B) AX / XB = AY / AC
(C) AX / YC = AY / XB
(D) AB / YC = AC / XB

Solution:
Given seg XY || seg BC
AX/BX = AY/YC [Basic proportionality theorem]
(BX/AX ) +1 = (YC/AY) +1
(BX+AX)/AX = (YC+AY)/AY
AB/AX = AC/AY
AB/AC = AX/AY
Hence correct option is (A).