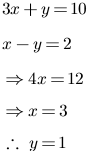(1) 2x + 3y = 12; x – y = 1
Solution:
Given
2x + 3y = 12
Substitute the values for x as shown in the table
| x | 0 | 6 | 3 |
| y | 4 | 0 | 2 |
Consider x – y = 1
| x | 1 | 0 | 2 |
| y | 0 | -1 | 1 |
Now plot the graph as shown below:
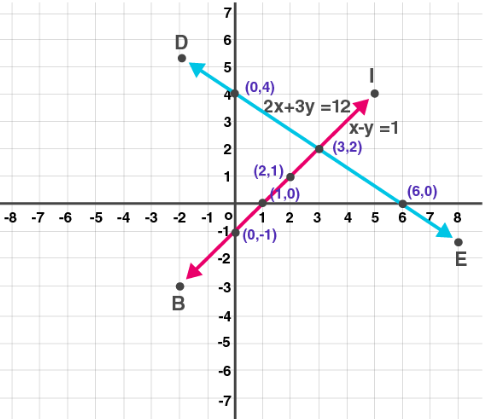
(2) x – 3y = 1; 3x – 2y + 4 = 0
Solution:
Given
x – 3y = 1
Substitute the values for x as shown in the table
| x | -2 | 4 | 1 |
| y | -1 | 1 | 0 |
Also given
3x – 2y + 4 = 0
| x | 0 | -2 | -4 |
| y | 2 | -1 | -1 |
Now plot the graph as shown below:
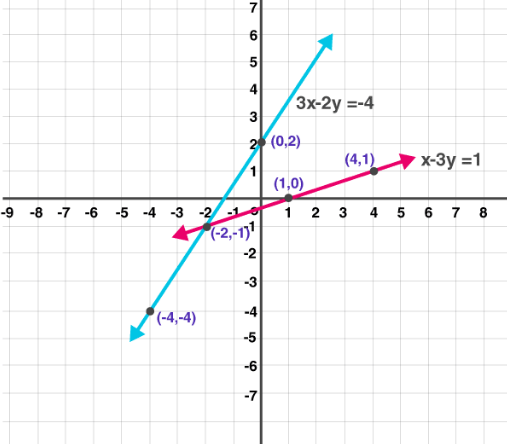
(3) 5x – 6y + 30 = 0; 5x + 4y – 20 = 0
Solution:
Given
5x – 6y + 30 = 0
Substitute the values for x as shown in the table
| x | 0 | -6 | 6 |
| y | 5 | 0 | 10 |
Also given
5x + 4y – 20 = 0
| x | 0 | 4 | 8 |
| y | 5 | 0 | -5 |
Now plot the graph as shown below:
(4) 3x – y – 2 = 0; 2x + y = 8
Solution:
For equation 1, let’s find the points for graph
3x – y – 2 = 0
At x = 0
3(0) – y – 2 = 0
⇒ y = -2
At x = 13
(1) – y – 2 = 0
⇒ y = 1At x = 2
3(2) – y – 2 = 0
⇒ 6 – y – 2 = 0⇒ y =4
Hence, points for graph are (0, -1) (1, 1) and (2, 4)
For equation 22x + y = 8
At x = 0y = 8
at x = 12
(1) + y = 8
⇒ y = 6
at x =42(4) + y = 8
⇒ y = 0
Hence, points for graph are (0, 8) (1, 6) and (4, 0)
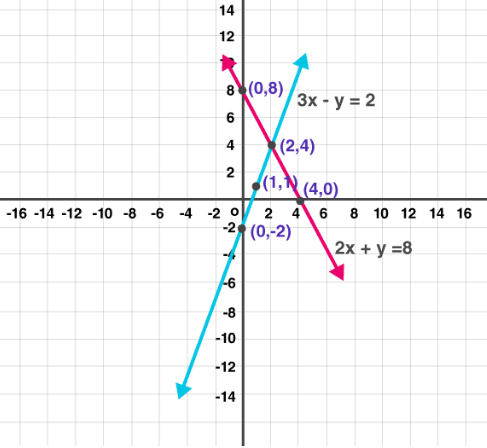
From graph, we observe both lines intersect at (2, 4)
Hence, x = 2 y = 4 is the solution of given pair
(5) 3x + y = 10; x – y = 2
Solution:
Given 3x + y = 10
| x | 1 | 2 | 3 |
| y | 7 | 4 | 1 |
Also, we have
x – y = 2
| x | 0 | 2 | 3 |
| y | -2 | 0 | 1 |
Solving Both equations