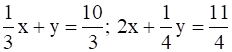(1) 3a + 5b = 26; a + 5b = 22
3a + 5b = 26 …… (i)
a + 5b = 22 ……… (ii)
Now by changing the sign of equation (ii) we get
– a – 5b = – 22
Subtracting equation (ii) from (i) we get
2a = 4
a = 4/2
a = 2
Substituting a = 2 in equation (ii) we get
2 + 5b = 22
5b = 22 – 2
5b = 20
b = 20/5
b = 4
∴ solution is (a, b) = (2, 4)
(2) x + 7y = 10; 3x – 2y = 7
Given
x + 7y = 10 ……. (i)
x – 2y = 7 ……… (ii)
Multiply equation (i) by 2 and equation (ii) by 7
2x + 14 y = 20
21x – 14 y = 49
Which implies
23 x = 69
x = 69/23
x = 3
Substituting x = 3 in equation (i)
3 + 7y = 10
7y = 10 – 3
7y = 7
y = 7/7
y = 1
∴ Solution is (x, y) = (3, 1)
(3) 2x – 3y = 9; 2x + y = 13
Given
2x – 3y = 9 …… (i)
2x + y = 13 …… (ii)
To subtract equation (ii) from (i)
Change the sign of equation (ii)
2x – 3y = 9
-2x – y = – 13
Which implies
– 4y = – 4
y = 4/4
y = 1
Substituting y = 1 in equation (ii)
2x + 1 = 13
2x = 13 – 12x = 12x = 6
∴ solution is (x, y) = (1, 6)
(4) 5m – 3n = 19; m – 6n = –7
Given
5m – 3n = 19 …… (i)
m – 6n = –7 …. (ii)
Multiply equation (ii) by 5
5m – 30n = -35 …. (iii)
Equating (i) and (iii), change the sign of equation (iii)
5m – 3n = 19
– 5m + 30 n = 35
Adding both we get
27n = 54
n = 54/27
⇒ n = 2
Substituting n = 2 in equation (i)
⇒ 5m – 3(2) = 19
⇒ 5m – 6 = 19
⇒ 5m = 25
⇒ m = 5
∴ Solution is (m, n) = (5, 2)
(5) 5x + 2y = –3; x + 5y = 4
5x + 2y = – 3 …. (i)
x + 5y = 4 …… (ii)
Multiply equation (i) by 5 and equation (ii) by 2
25 x + 10 y = -15 …. (iii)
2x + 10 y = 8 …. (iv)
Change sign of equation (iv)
25 x + 10 y = -15
– 2x – 10 y = – 8
23 x = -23
x = -1
Substituting x = –1 in equation (ii)
– 1 + 5y = 4
5y = 4 + 1
5y = 5
Y = 1
∴ solution is (x, y) = (–1, 1)
(6)



(7) 99x + 101 y = 499; 101x + 99y = 501
Solution:
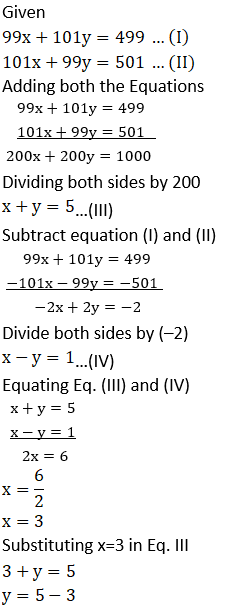

(8) 49x – 57y = 172; 57x – 49y = 252
Solution: